円と球 小学3年生の円と球プリントです。 こちらのプリントでは一部コンパスを使用した作図問題があります。 正確な長さを作図する能力が求められますので、 必ず100%の比率で印刷(倍等印刷)して下さい。 そうしないと1cm角のマス目が08cm角など中途円の面積の求め方を一通り身につけたら、少し応用的な問題にも挑戦してみましょう。 円の面積の応用問題をやってみよう 円の面積の、もっと基本的な問題のノート例はこちらです。 円の面積その1 それでは、 小学6年生で習う、円の面積の問題の解き方を世界一やさしく解説します。 ★今から学ぶこと 1、円の面積を求める式円の面積=半径×半径×314 2、円の一部の面積を求める式円の面積の一部=半径×半径×314×中心の角/360° 3、色(かげ)がついた部分の面積の求め方全体白い部分 ★こ

円周率を使って 円の周囲の長さを計算する自主学習ノートを作りましょう 小数のかけ算を使います 5年生の後半から 6年生におすすめの自主学習です 円 半 円 おうぎ形の周囲の長さを計 学習 小学校 算数 中学数学
円の面積の求め方 応用
円の面積の求め方 応用- 円の面積の公式はご存じの通り、πr 2 である。 πは円周率、rは半径だ。 ではなぜ、この式になるのだろうか。 様々な証明方法があるが、まず円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さ
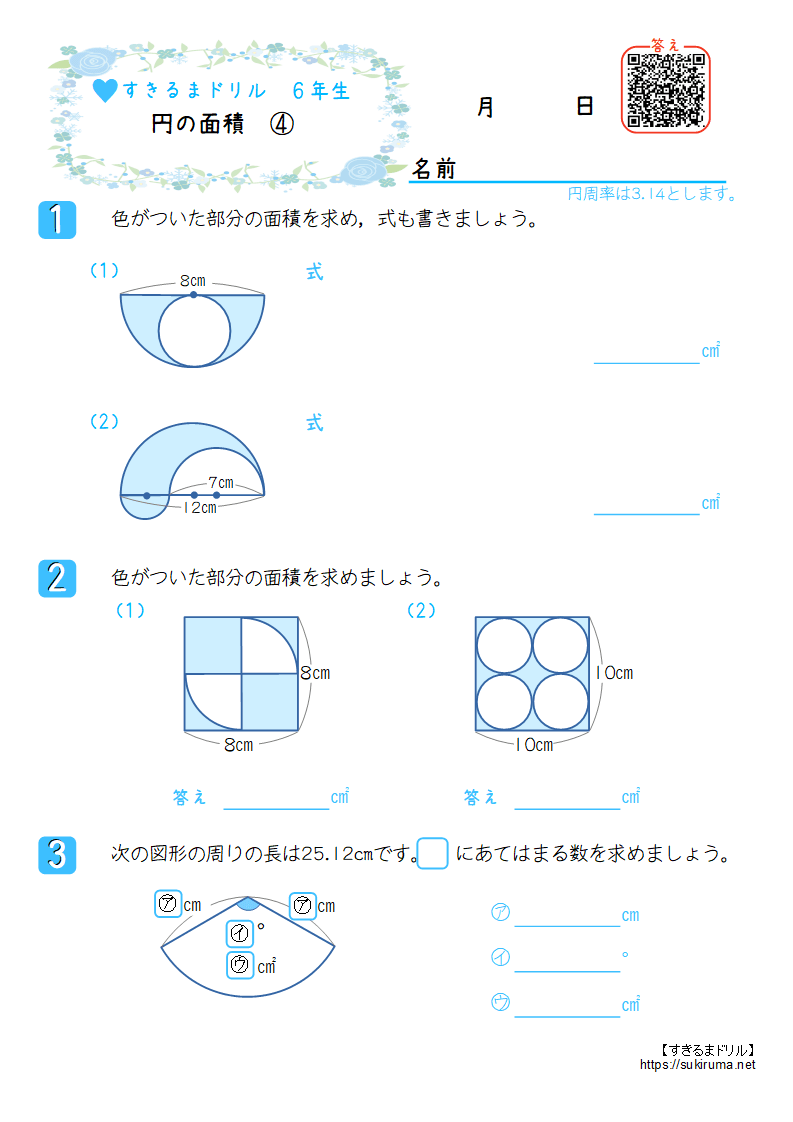



すきるまドリル 小学6年生 算数 円の面積 無料学習プリント すきるまドリル 無料学習プリント
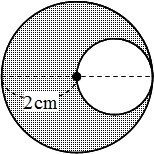
弓形の面積(弓形の半径と高さから) 本ページ項以外にも多々利用させていただいています,エクセルでの計算結果検証に使え,ありがたいです! ! 。 顧客より頂いた図面では,玄長・円弧表示がなく高さと半径から求められるのは,私の需要に次の図のように半径10(cm)の円の中に半径5(cm)の円が2つ接しているとき,斜線部の面積(cm 2) ヒント 図のように小さい円の半分を回転させると,凸の部分がちょうど凹の部分に重なるから,大きい円の面積の半分を求めるとよい円の面積を求める公式は、S = πr^2 で表されます。このページでは、円の面積の求め方を、計算問題と共に説明しています。また、公式の導き方のイメージも説明しています。
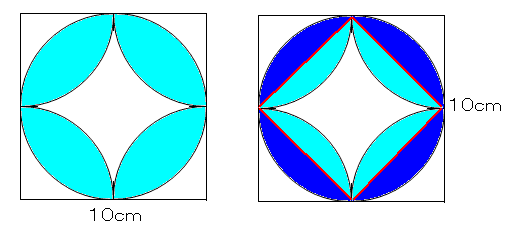
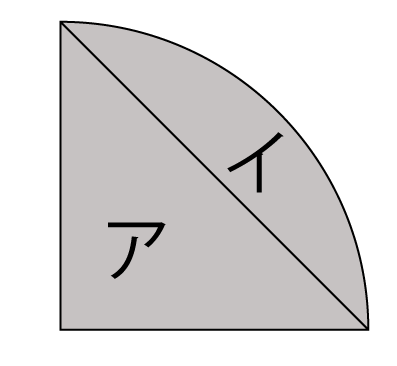
円周率が314の時、下の図の アとイの面積比は1:057 となる。 半径が10cmの場合で考えると アの面積は 10×10÷2=50(㎠) イの面積は 10×10×314÷4ー50 =285 (㎠)6年「円の面積」 氏名 1 次の円の面積は何㎠ですか。 ⑴ 半径4cmの円 半径 × 半径 × 314 = 円の面積 式 答え ⑵ 半径8cmの円 式 答え ⑶ 直径14cmの円 直径 ÷ 2 = 半径 式 半径 × 半径 × 314 = 円の面積 答え ⑷ 直径18cmの円 式 答え 円の面積の求め方を一通り身につけたら、少し応用的な問題にも挑戦してみましょう。 円の面積の応用問題をやってみよう 円の面積の、もっと基本的な問題のノート例はこちらです。 円の面積その1 それでは、
外接円の半径と三角形の面積の関係(S=abc/4R) 三辺の長さが a, b, アポロニウスの円の証明と応用 四角形の重心の2通りの求め方 多角形の面積の求め方 長方形=縦×横 正方形=1辺×1辺=対角線×対角線÷2 平行四辺形=底辺×高さ 台形=(上底+下底)×高さ÷2 ひし形(対角線直交四角形)の面積=対角線×対角線÷2 三角形=底辺×高さ÷2 円の面積の求め方解説 円の面積の求め方 name NO1 応用問題-① 中 NO1 miss 1 開始日 終了日 ヒント 円周÷314=直径 直径÷2=半径 半径×半径×314=円の面積 ヒント 半径×半径×314÷ =面積 360÷60 360÷72 ⑤,⑥,⑦のヒント ひし形の面積=対角線×対角線÷2



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋



実践記録算数5年
円の面積は (半径)×(半径)×(円周率314) という公式になるわけですね! 円の面積、円周の求め方練習問題 それでは、円の公式について学んだところで次は実際に計算ができるように練習してみましょう。円の面積の求め方を自主学習ノートで復習しましょう。 円の面積の基本的な練習問題 円の面積の求め方を確認しておきます。 円の面積=半径×半径×円周率 ちなみに、円周の長さの求め方は、 円周の長面積比を使った問題(中級編) 次の図で、 であるとき次の問いに答えなさい。 (1) と の面積比を求めなさい。 (2) と台形 の面積比を求めなさい。 なので、このように別々に書いてあげると見やすくなりますね。 この2つの三角形は相似になって




はっぱ型 の図形の面積 身勝手な主張




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく
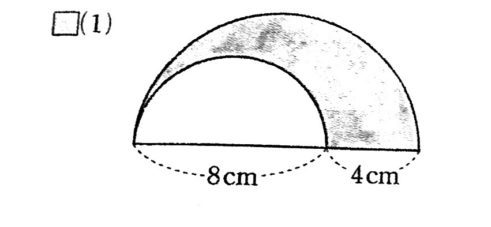
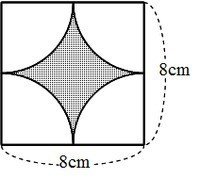
おうぎ形の弧の長さと面積の求め方|小学生に教えるための解説 管理人 10月 5, 18 / 11月 26, 18 おうぎ形は『円』と『比』の単元が関係するため、両方をしっかり抑えていないと理解することができないでしょう。 円周率と円周(応用) いろいろな円周を含む周りの長さを求める応用問題です。 半円の周りの長さや、円や図形を組み合わせた問題などが出題されます。 簡単な問題が出来るようになったら、中学入試レベルの応用問題も取り組んでみてください。 円を2つ合わせた面積を求める 色のついた部分の面積を求めます。 大きい円の面積から小さい円の面積をひきます。 別々に求めても構いませんが計算式を1つにした方が早く答えを求めることが出来ます。 8×8×3144×4×314 = 64 ×314 16 ×314 = (64−16



6年算数 円の面積 2 わかる教え方




円の面積 応用1の解説 春日井市高蔵寺の学習塾 西村セミナールーム
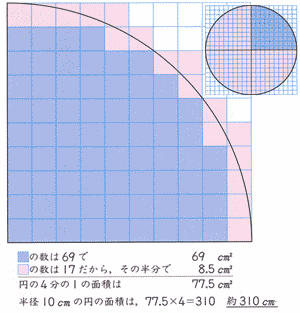
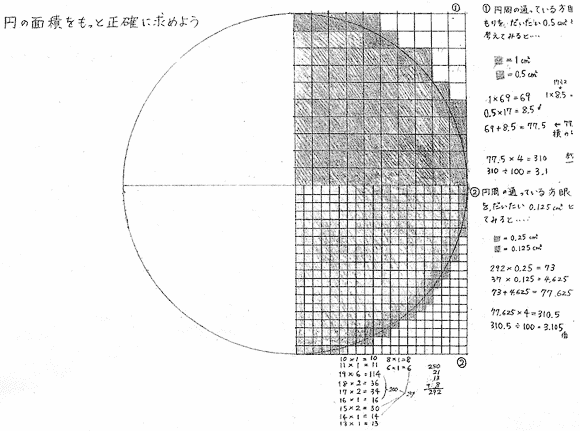
高校数学Ⅲ 積分法の応用(面積・体積・長さ) 積分の一大目標は、図形の面積・体積・長さを求めることである。 数Ⅱでも学習したが、非常に基本的なものに限られていた。 数Ⅲでは様々な関数が登場し、また単純な積分計算では済まない複雑な図形もする正方形の面積よりも大きく, 外接する正方形より小さいことから, 円の面積が半径× 半径の2倍より1大きく,4 倍より小さいことを理解させる。 その後, 実際に4の円の方眼を数える活動を通し円の面積から半径を求める 円の面積から直径を求める 円の面積から円周を求める 使用しているスクリプトの特性から、特に少数点以下の計算結果に誤差が出る場合があるようです。
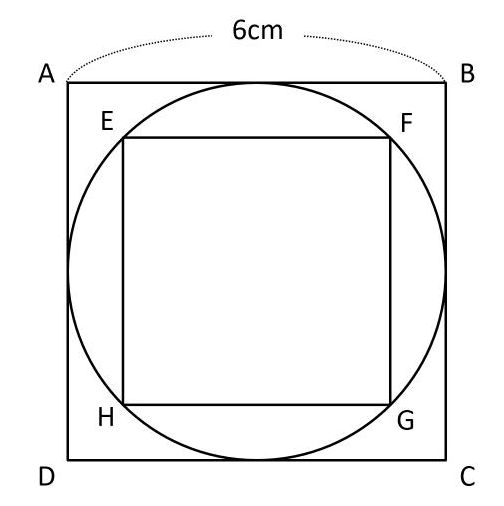



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ



算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素
(ア) 応用する活動として,円の の形や三角形などに着眼させ,既習の面積の求め方を使って図形の 面積の求め方について考えさせる。 (イ) 説明する活動として,面積を求めた式から,その考え方を読み取り,式や図や言葉を使って説明させ基本的な解き方 「半径が等しいおうぎ形のポイント」を利用した解き方 360×157/628=90 答え 90 ° 工夫した解き方 特殊な問題を除くと、 円周や弧の長さ、円の面積やおうぎ形の面積は 「円周率の倍数 」です。 円の面積の求め方って あれって結局縦×横の応用なんだってね。 円を ケーキ を切るみたいな感じでN等分して交 差し ながら並べると上辺と下辺がボコボコと起伏した 平行四辺形 になるで




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学
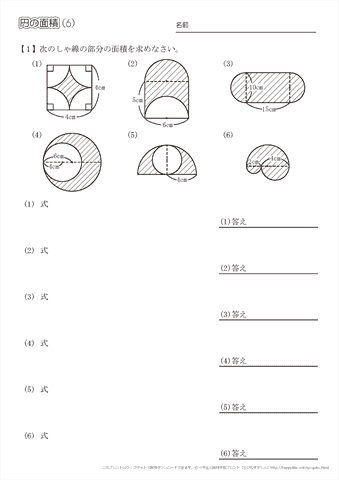



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
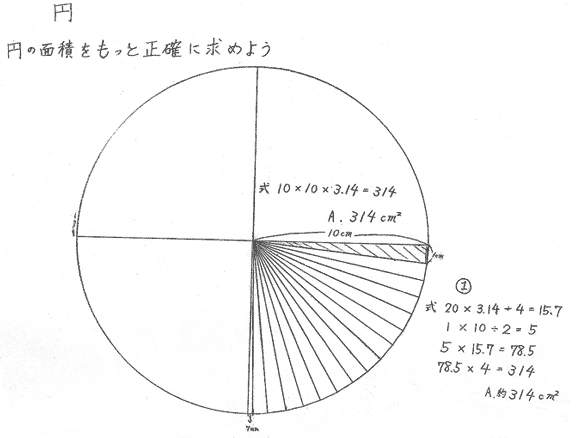



実践記録算数5年
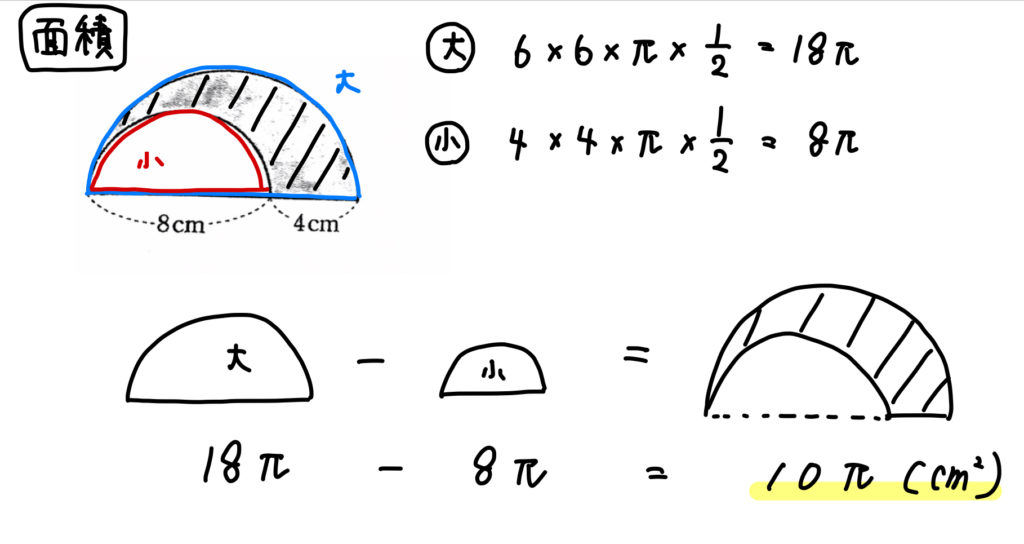



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ



実践記録算数5年



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ



世界一やさしい 円の面積を求める問題の解き方 Shun Ei Note
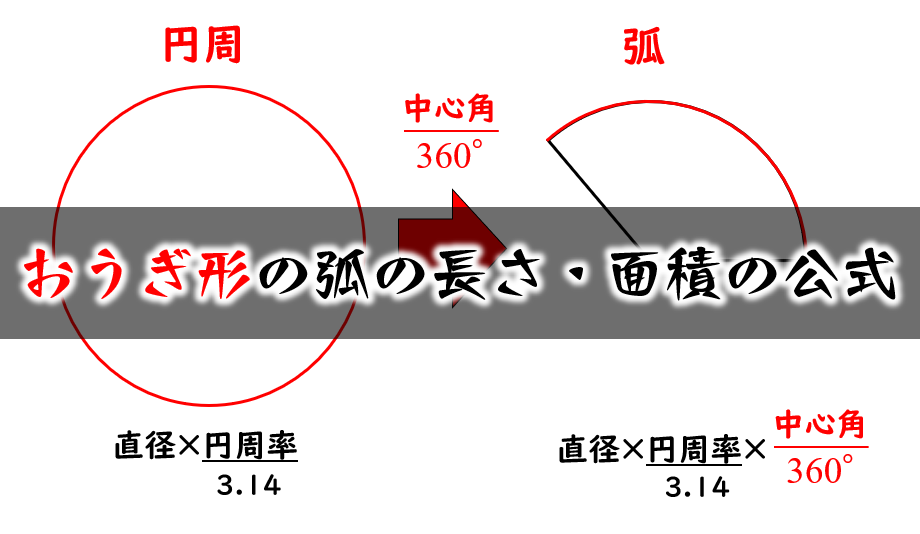



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




応用問題 答え Clear
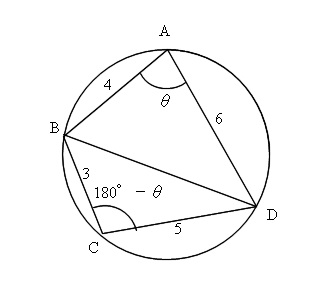



円に内接する四角形の面積の求め方と定理の使い方




扇形の面積の求め方 公式と計算例




円の面積 円周の求め方 公式 小学生 中学生の勉強




面積の求め方 算数の教え上手 学びの場 Com
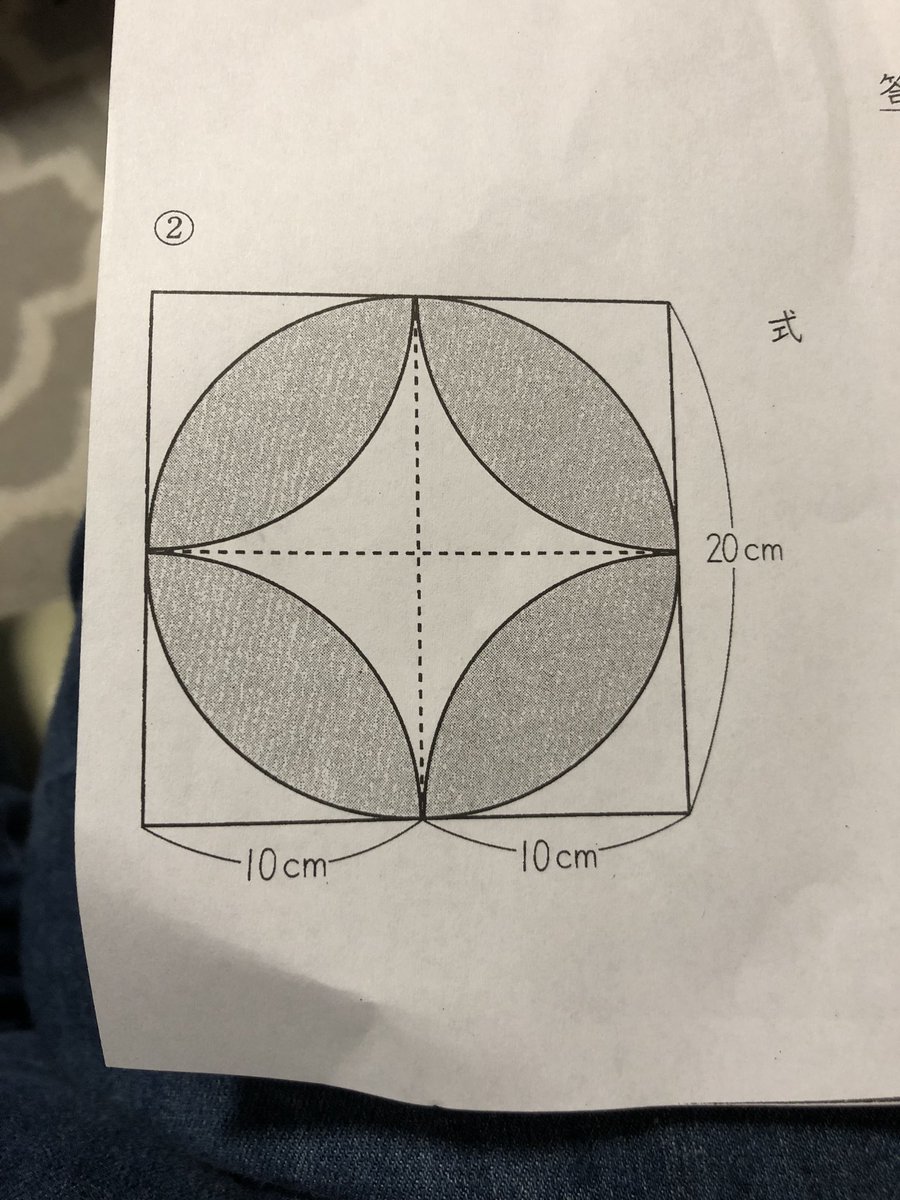



円の面積



1
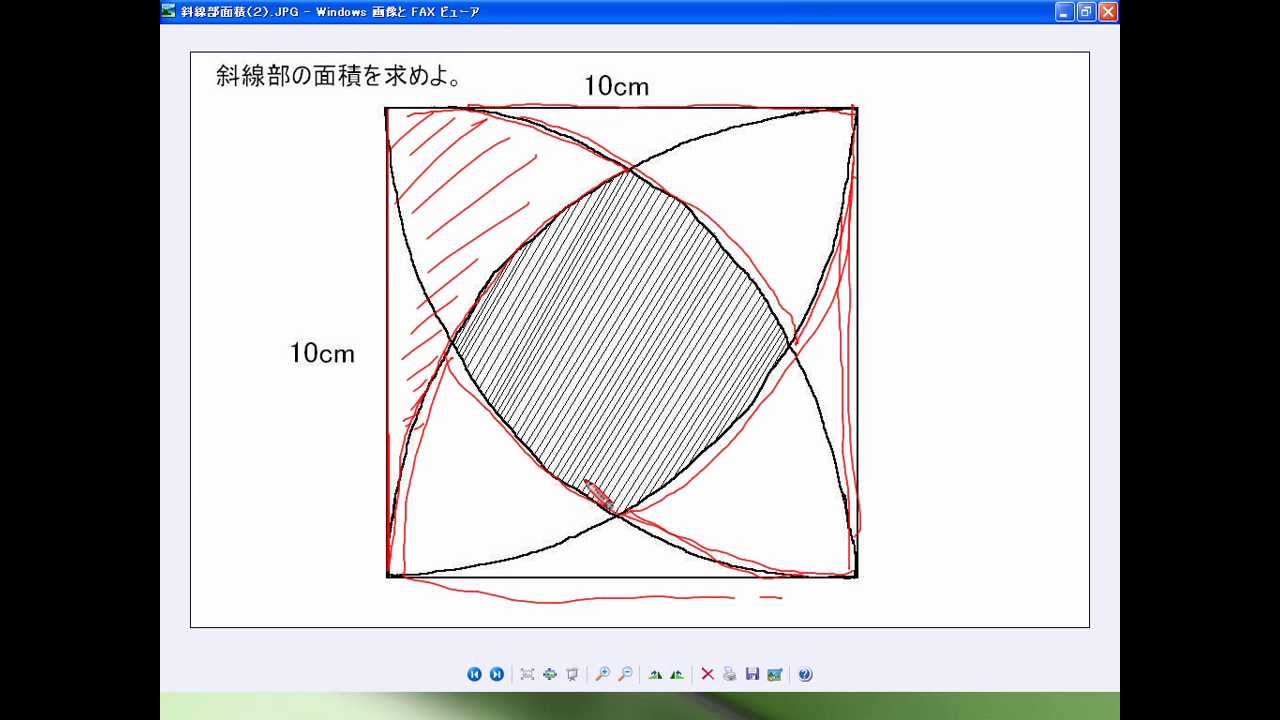



斜線部の面積 4 1辺10cmの正方形の場合 Youtube
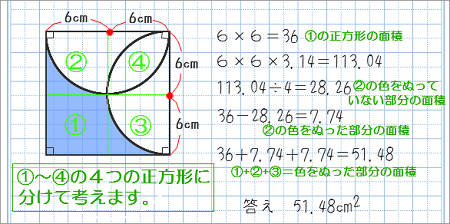



円の面積 その2 家庭学習レシピ



世界一やさしい 円の面積を求める問題の解き方 Shun Ei Note




円の面積 円周の求め方 公式とやり方を解説 小学生向け 中学数学 理科の学習まとめサイト




数学の伝道師 秋山仁さん 算数を勉強しないと損 子どもを算数好きに育てるには 親子で挑む 算数つまずき攻略法 朝日新聞edua
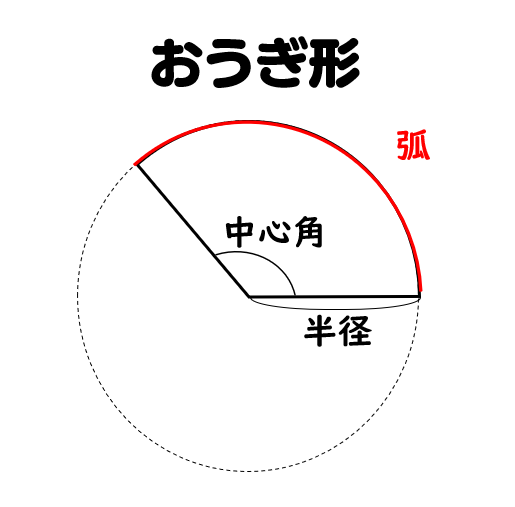



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun



算数 三日月形 半円 の面積の応用問題の答 なるほどの素




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア
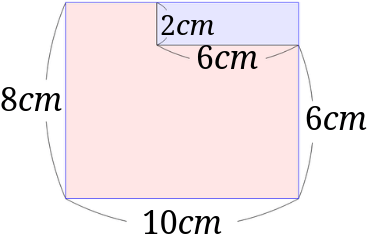



小学4年生で習う長方形や正方形の面積の応用問題を解説 みけねこ小学校




円周率を使って 円の周囲の長さを計算する自主学習ノートを作りましょう 小数のかけ算を使います 5年生の後半から 6年生におすすめの自主学習です 円 半 円 おうぎ形の周囲の長さを計 学習 小学校 算数 中学数学




円の面積 練習応用 Youtube
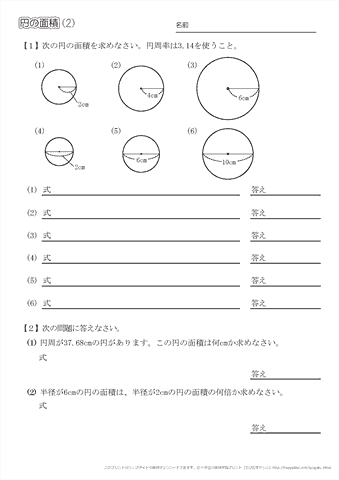



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
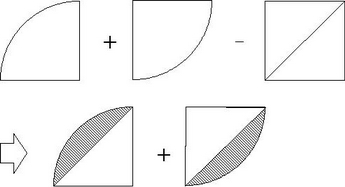



0 57の暗記 を活用しよう 前田昌宏の中学受験が楽しくなる算数塾
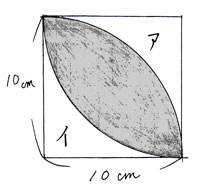



円の面積 応用1の解説 春日井市高蔵寺の学習塾 西村セミナールーム




中学受験 算数 面積 よく出る応用問題や難問をわかりやすく解説 中学受験アンサー




円周の求め方と円の面積について アタリマエ




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題
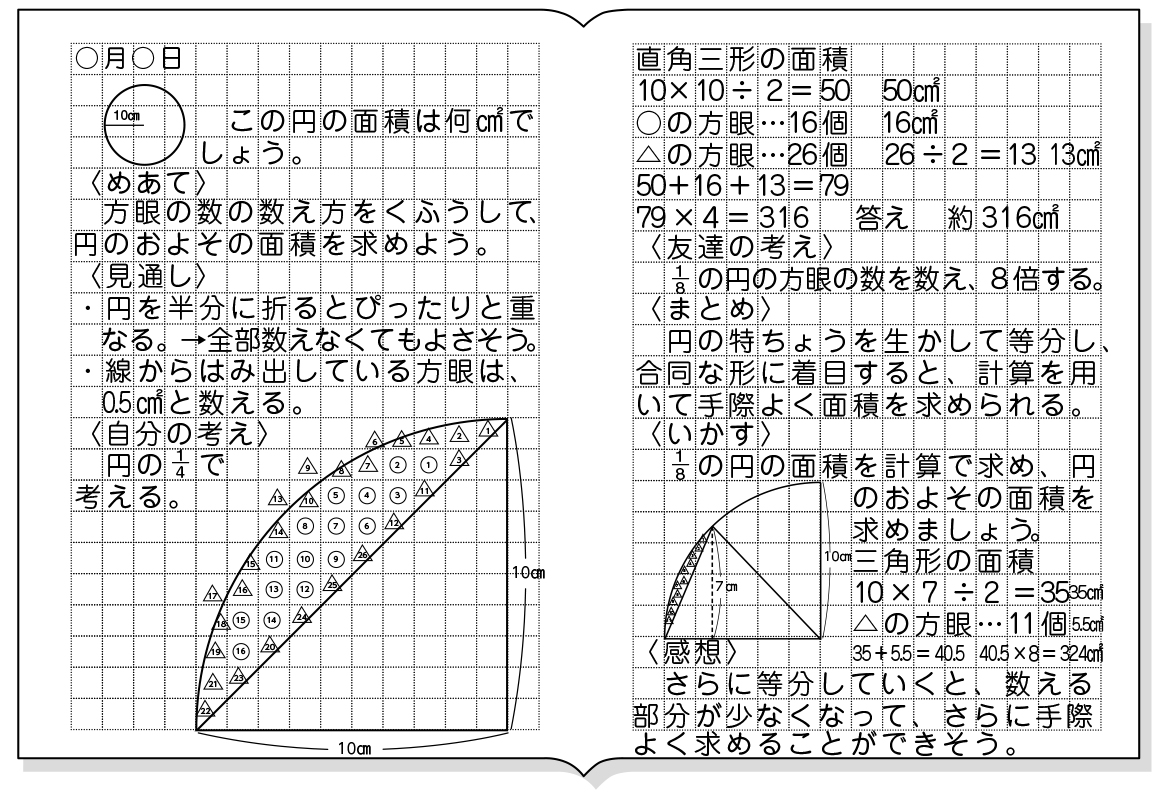



小6算数 円の面積 指導アイデア 1 みんなの教育技術



小学6年生の面積の問題です 求め方がわからないので 教えてください よ Yahoo 知恵袋




応用 おうぎ形と正方形の面積 なかけんの数学ノート
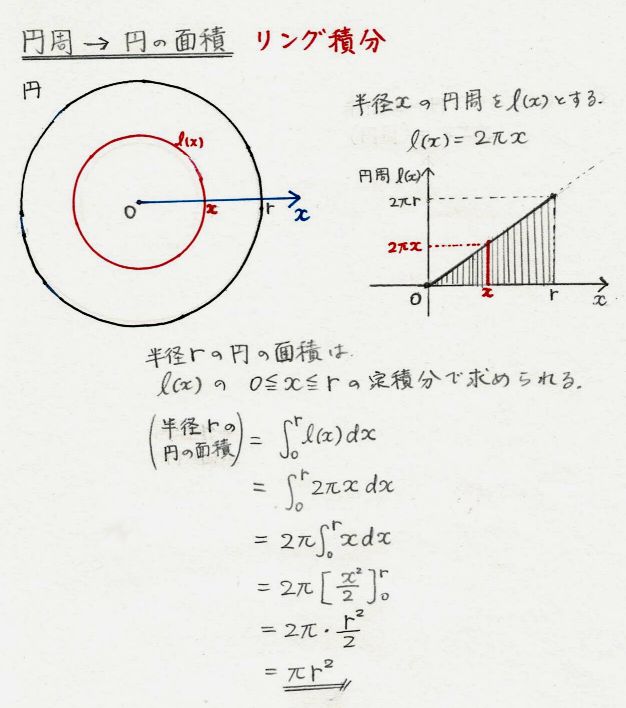



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




小6 算数 小6 2 円の面積 応用編 Youtube




弓形の面積 香料ゐっすゐの夢



面積 これが中学入試に出た図形問題



Www Pref Hiroshima Lg Jp Uploaded Attachment Pdf
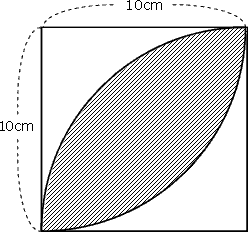



面積の求め方 算数の教え上手 学びの場 Com



横の図の色がついた面積の求め方をどなたか教えてください すみません Yahoo 知恵袋




円とおうぎ形 応用 無料で使える中学学習プリント




ボード 豆知識 のピン
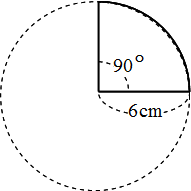



世界一やさしい 円の面積を求める問題の解き方 働きアリ




小6 算数 小6 旧 円の面積 Youtube
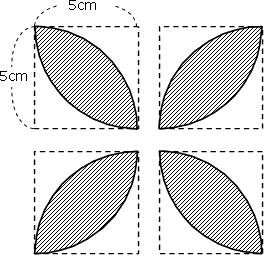



面積の求め方 算数の教え上手 学びの場 Com




円の面積の応用 小学校6年算数より 身勝手な主張




山と数学 そして英語 小学校算数 円の面積に関する応用問題




円の面積 円周の求め方 公式とやり方を解説 小学生向け 中学数学 理科の学習まとめサイト
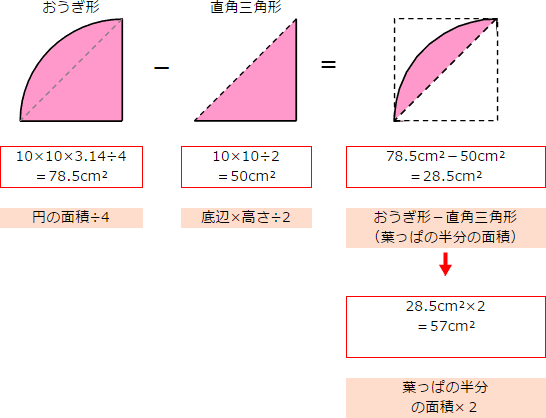



面積の求め方 算数の教え上手 学びの場 Com
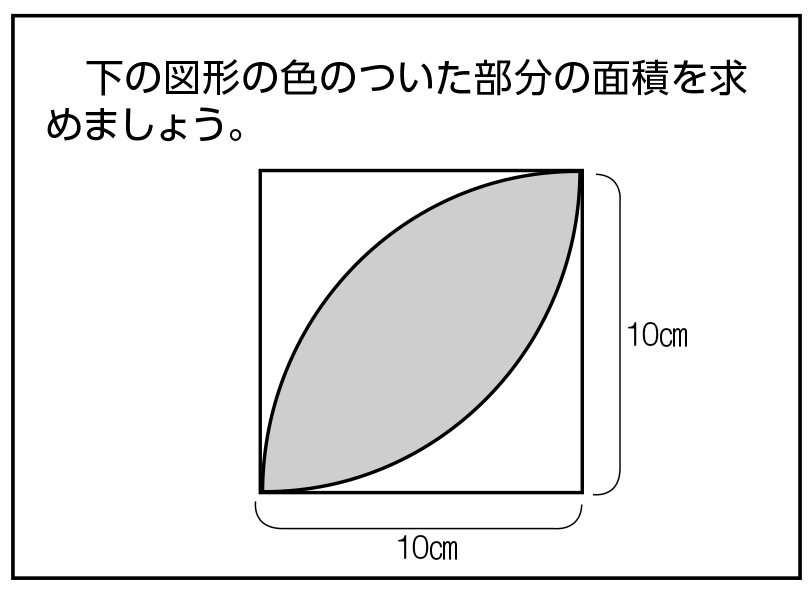



小6算数 円の面積 指導アイデア 2 みんなの教育技術
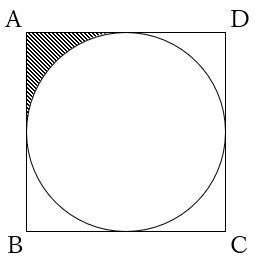



半径の分からない円の面積 中学受験プロ講師ブログ
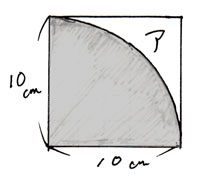



円の面積 応用1の解説 春日井市高蔵寺の学習塾 西村セミナールーム
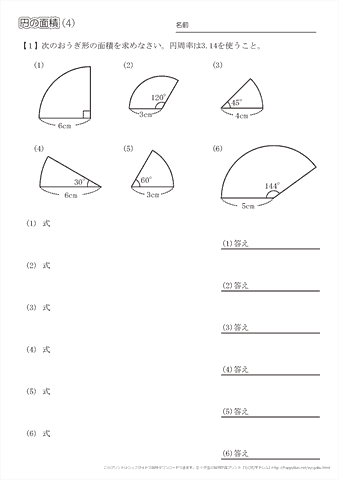



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
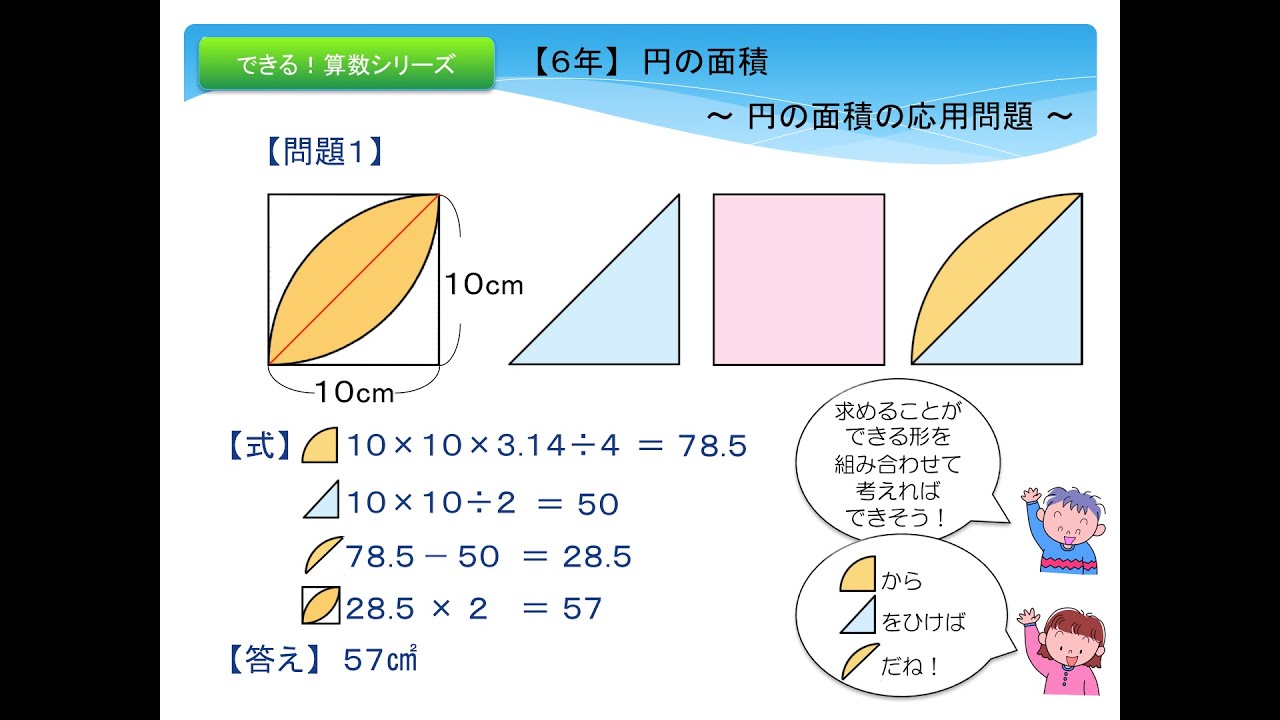



スマホok 6年 円の面積 円の面積の応用問題 Youtube




おうぎ形に関する応用問題3選
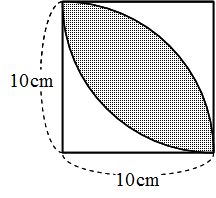



世界一やさしい 円の面積を求める問題の解き方 働きアリ



Usrlawlzpzk2hm




すきるまドリル 小学6年生 算数 円の面積 無料学習プリント すきるまドリル 無料学習プリント



1
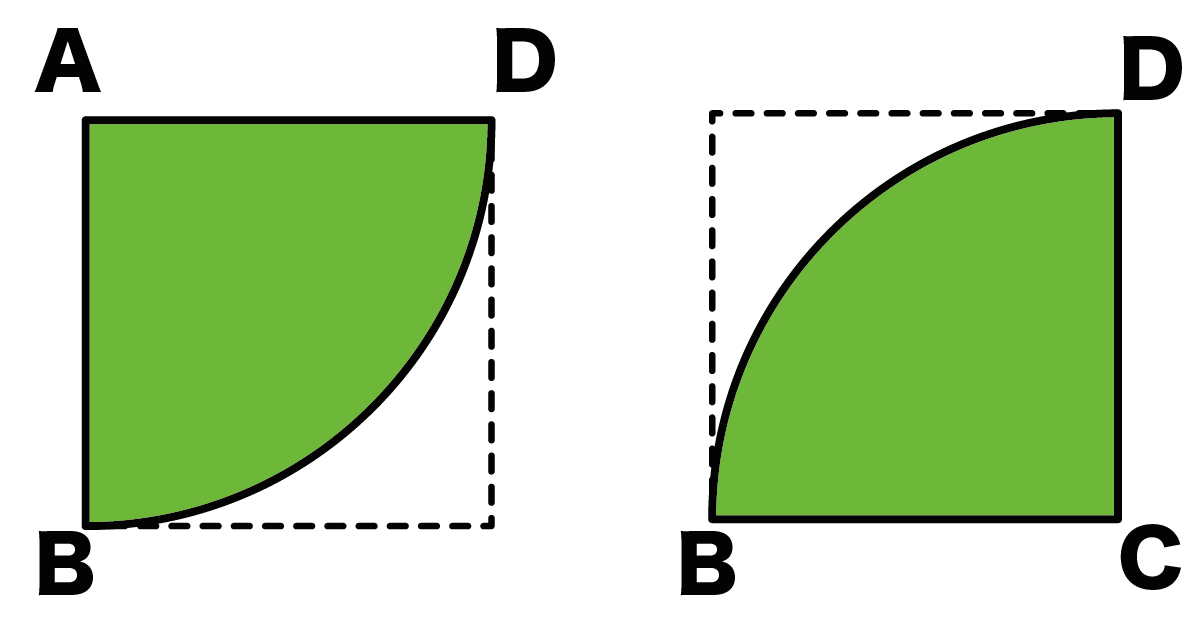



正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




半円を回転させる面積の問題 プリントを使って自分で解こう
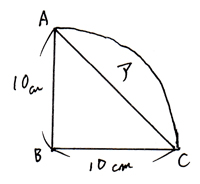



円の面積 応用1の解説 春日井市高蔵寺の学習塾 西村セミナールーム
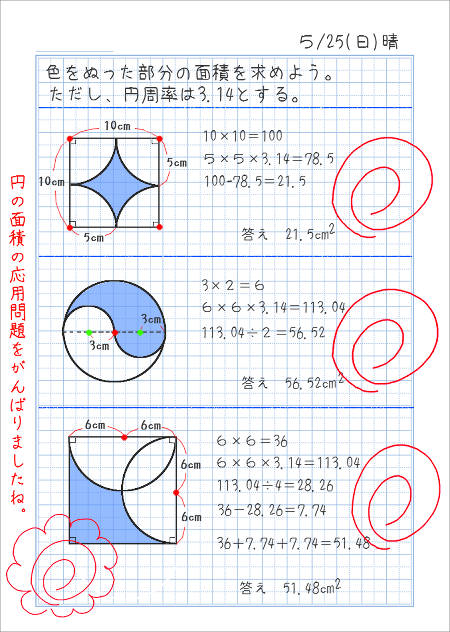



円の面積 その2 家庭学習レシピ
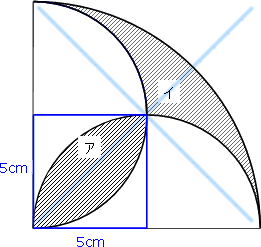



面積の求め方 算数の教え上手 学びの場 Com
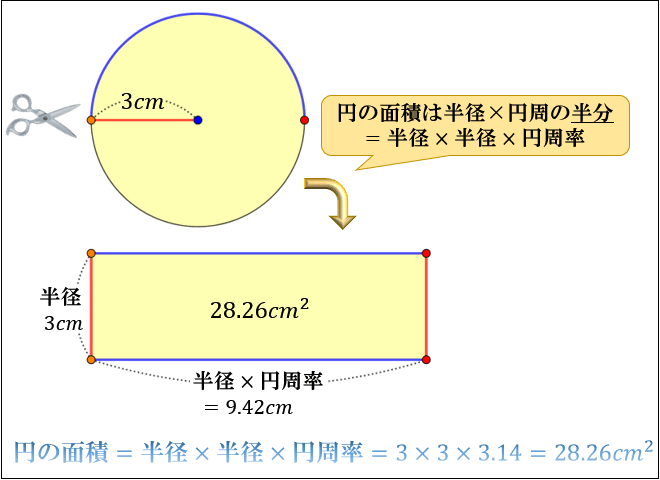



円周の求め方と円の面積について アタリマエ




すきるまドリル 小学6年生 算数 円の面積 無料学習プリント すきるまドリル 無料学習プリント




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト
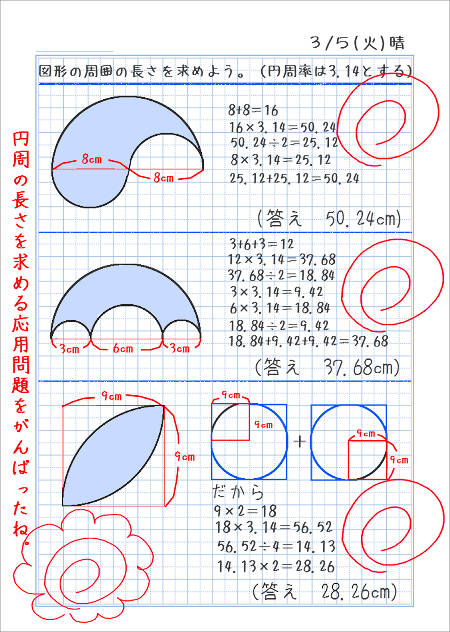



円周の長さの問題をもっと解いてみよう 家庭学習レシピ
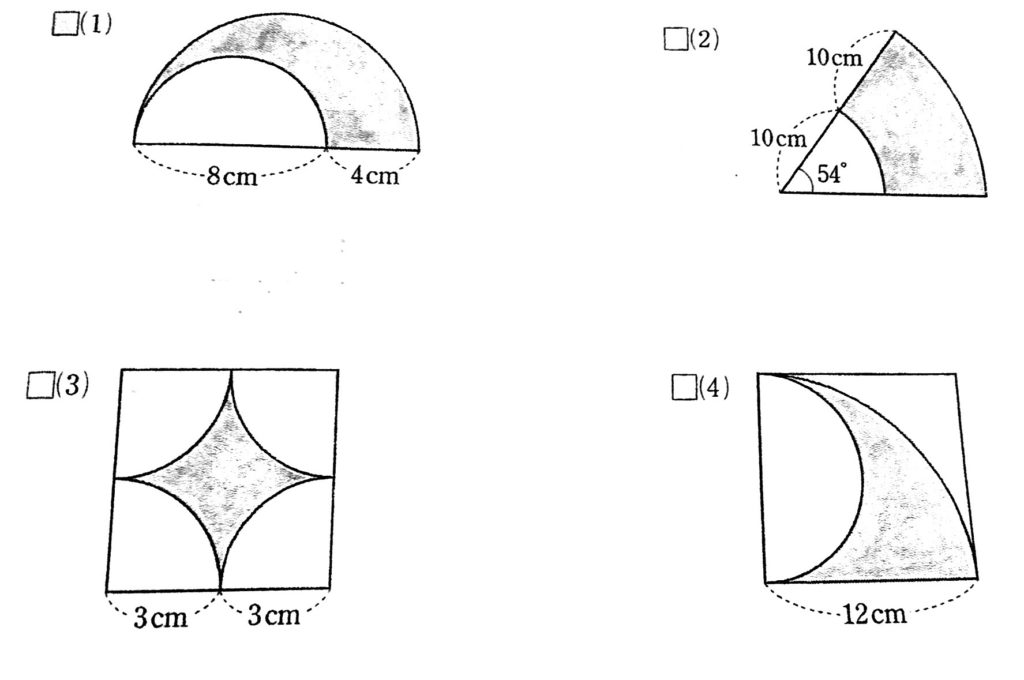



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ



面積分




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




円 扇形 の面積 周や弧の長さの公式 数学fun



パワーポイント教材 那須烏山市立烏山小学校




標準 おうぎ形と正方形の面積 なかけんの数学ノート
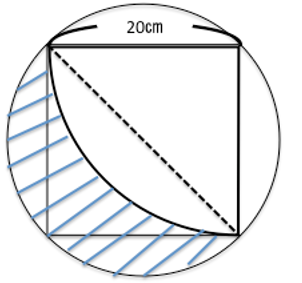



円の半径がでない問題の攻略法 中学受験プロ講師ブログ
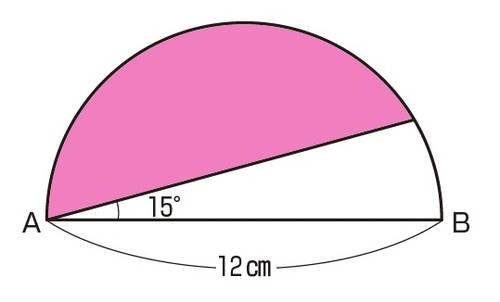



灘 開成 麻布 超難関校に挑戦 円周率 の引っかけ問題 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン
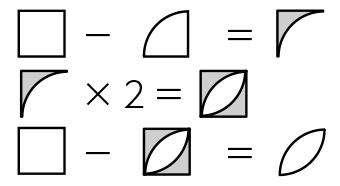



小6算数 円の面積 指導アイデア 2 みんなの教育技術



算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素




円の面積の求め方 公式と計算例




円の面積 その2 家庭学習レシピ




円 扇形 の面積 周や弧の長さの公式 数学fun



Q Tbn And9gct8mjpenhvsxxfek Ceorhkk1e5jnkqcmelwl1yafnkyt4mflap Usqp Cau



3




はっぱ型 の図形の面積 身勝手な主張




円の面積 その2 家庭学習レシピ




6年算数 円の面積 なぜ 半径 半径 円周率になるのか 解説します Youtube
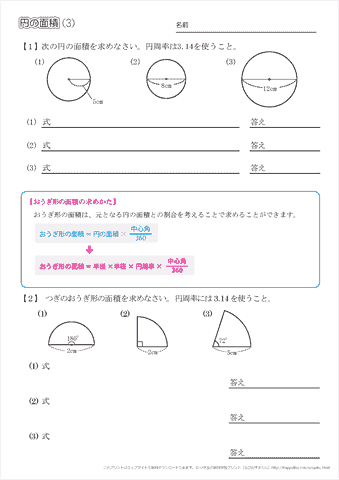



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
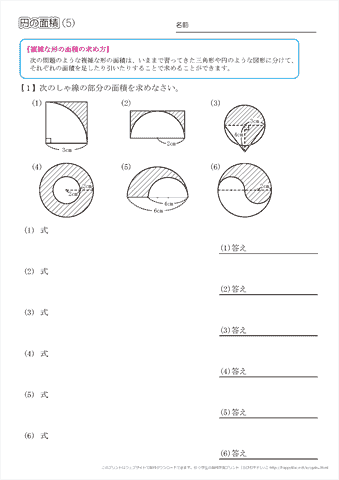



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
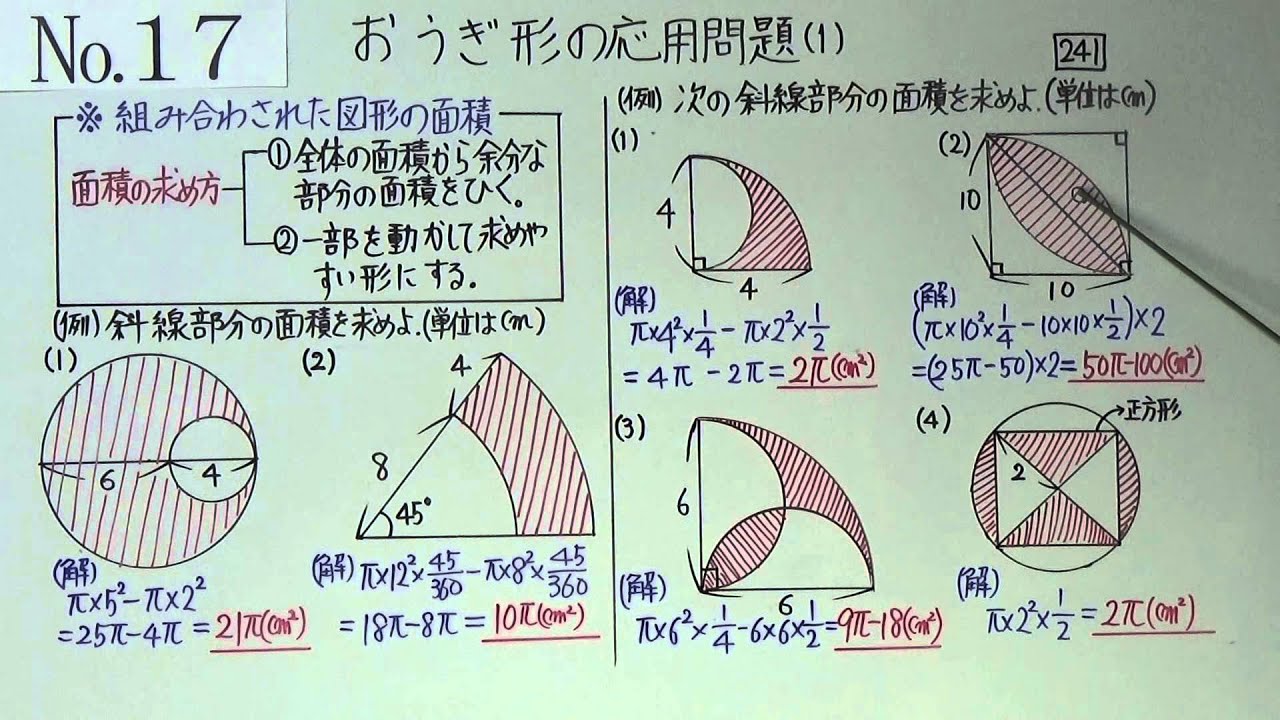



中1 17 2 おうぎ形の応用 1 Youtube


